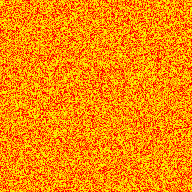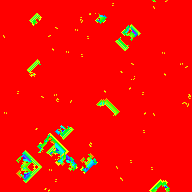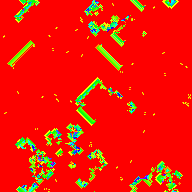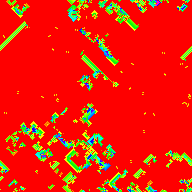Subset Sum Automata
WARNING: Contains brightly colored, rapidly flashing patterns. Best viewed in Chrome.
Subset sum automata are a family of cellular automata based on the subset sum problem. They're on a square grid like Conway's Game of Life, but instead of each cell being just on or off, the state is a nonnegative integer:

A subset sum automaton is defined by three integer parameters: a target offset, a reward, and a penalty. At each time step, each cell determines its target number by adding the target offset to its own value and checks its orthogonal and diagonal neighbors to see if any subset of them sum to this number. If such a subset exists, the reward is added to the cell. If not, the penalty is subtracted from the cell.
The above image comes from the +3/1/1 automaton, meaning the target offset is +3, the reward is 1, and the penalty is 1. Some examples:

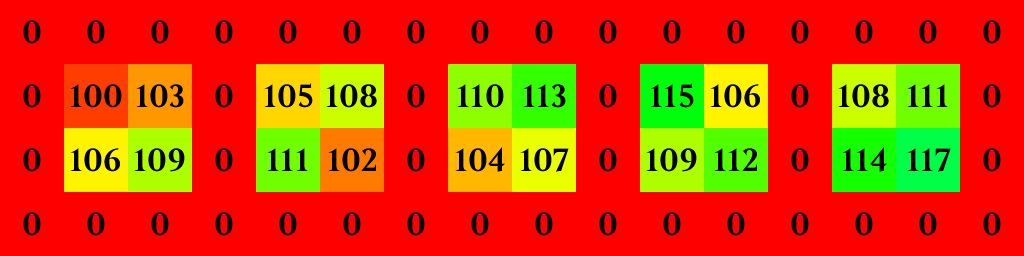
The target number for this cell is 14 (11+3). There's only one subset of its neighbors which sum to 14 — the two 7s — but that's enough for it to earn its reward. This cell's value will increase by the reward (1) to 12 next generation.
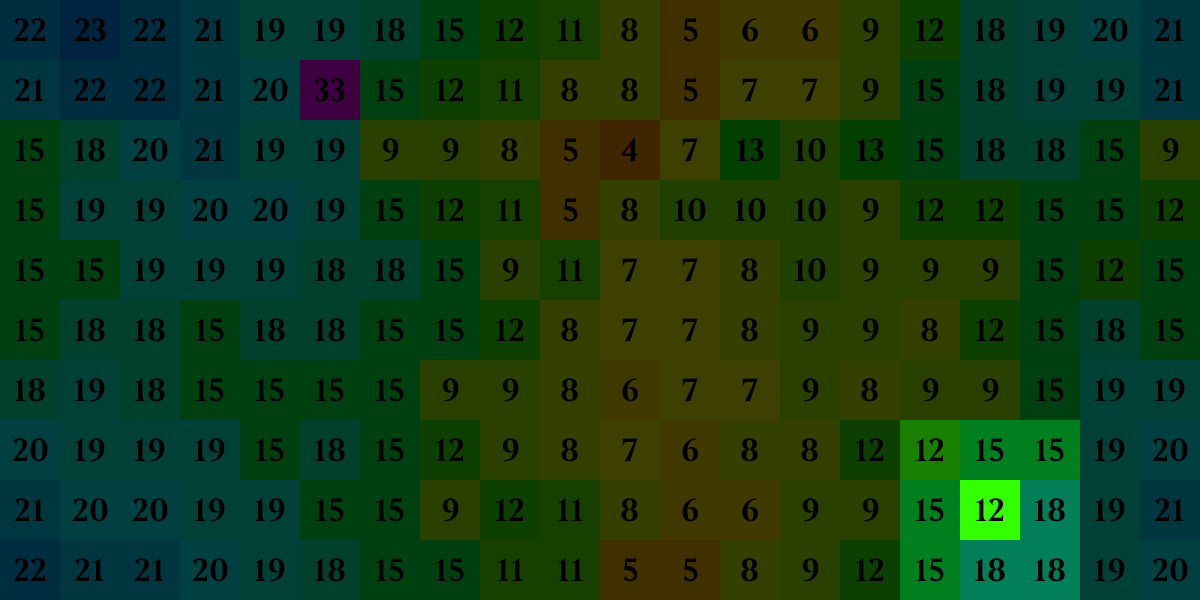
The target for this cell is 15 (12+3), and there are four subsets of its neighbors that sum to 15: each of the 15s by themselves. This cell's value will increase by the reward (1) to 13 next generation.
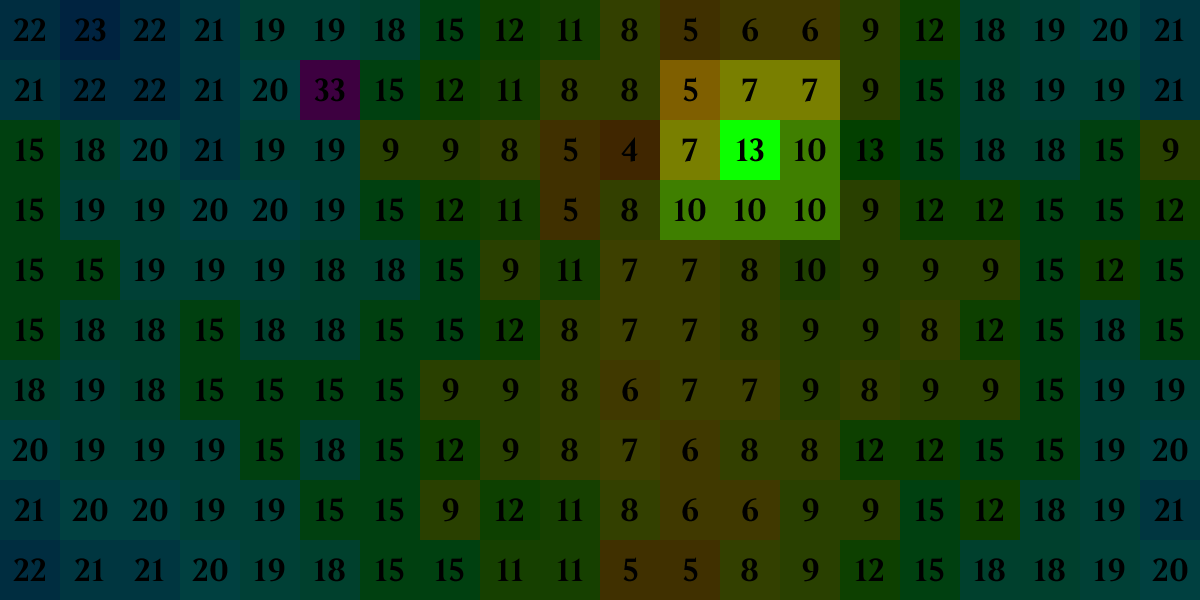
The target for this cell is 16 (13+3) and, although there are subsets of its neighbors that sum to 15 and 17, there's no subset that sums to 16. This cell's value will decrease by the penalty (1) to 12 next generation.
Here's what it looks like running from a random seed:

Many subset sum automata have this chaotic, pulsating appearance. Clusters of low values tend to increase, since it's easy to sum them together to whatever target number you're trying to reach, and clusters of high values tend to decrease because they don't have access to smaller neighbors that get them to the exact value they need. In +3/1/1, the penalty is low enough that even when the values of the fan-like structures become too large and they begin to collapse, they stick around until the low-value medium around them aligns in such a way that they can grow again. Often, they don't collapse and instead grow forever, more on that later...
+3/1/1 doesn't look Life-like: there are no still lifes, no oscillators, and no spaceships. Still lifes aren't possible when cells are being either rewarded or penalized every turn; oscillators, though, we can do. Here's one with period 4 in +5/4/7:

And a c/2 orthogonal spaceship — the smallest possible, as far as I know — in +7/3/2:

Ships like this exist in all rules of the form +(2x+1)/x/x-1 for x >= 3. They are extremely simple, the gliders of subset sum automata, but nowhere near the most common in the scope of all rules. Much more common are c/8 orthogonal ships like this one from +12/5/9:

Despite its complexity — central cells iterate through 26 states before hitting zero for the last time — it's ubiquitous in its rule. Even more exotic ships, however, can be found with larger parameters. In +123/53/12, this strange, naturally occurring creature is mod 201 and moves diagonally at 25c/402:

Between the Life-like and the un-Life-like, plenty of variety can be found by fiddling with the target offset, penalty, and reward:





You see the most interesting results when the reward and penalty are coprime; this way any cell can eventually come to have any value. Less interesting would be something like +10/2/4; odd-valued cells would always stay odd, and the evens would stay even. On the subject of undesirable parameters, it's easy to create rules that tend towards divergent patterns that, while nifty in their own right, are really just numbers getting larger in larger in a predictable way. Rules with a higher reward than penalty have a good chance of diverging (but won't always, as some of the rules above show). A low target offset also increases the odds of divergence. An example is +1/1/1, where a small seed of alternating 1s and 0s can grow adjacent cells to arbitrarily large values:

Which can "crystallize" a gradient of values that always have a neighbor one higher than themselves, which happens to be their target number:

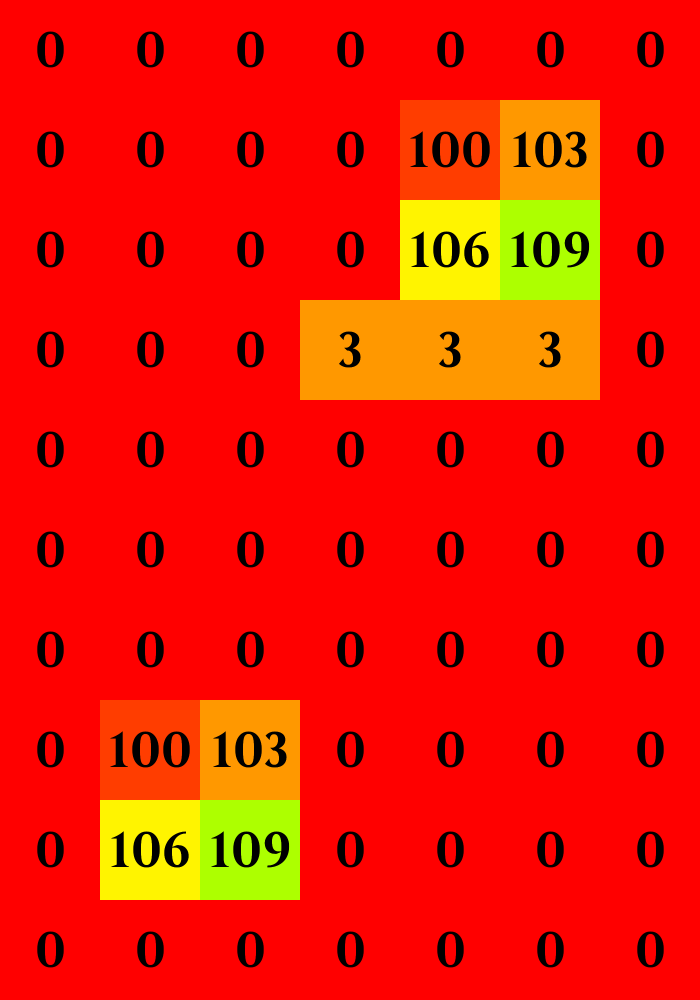
Another type of divergent pattern never grows in population but nevertheless reaches arbitrarily large values, like this small square in +3/5/7:
Unlike their plane-devouring brethren, these bounded divergent clusters can be useful for pattern construction. They're nearly impossible to disrupt and their values are only ever fit for summing to their own target numbers, meaning that as far as their neighbors are concerned, they're worthless for summing to moderate values and might as well be locked at 0. This ability to "shut off" cells makes for readily controllable machinery, as in this +3/5/7 gun derived from naturally occurring patterns:

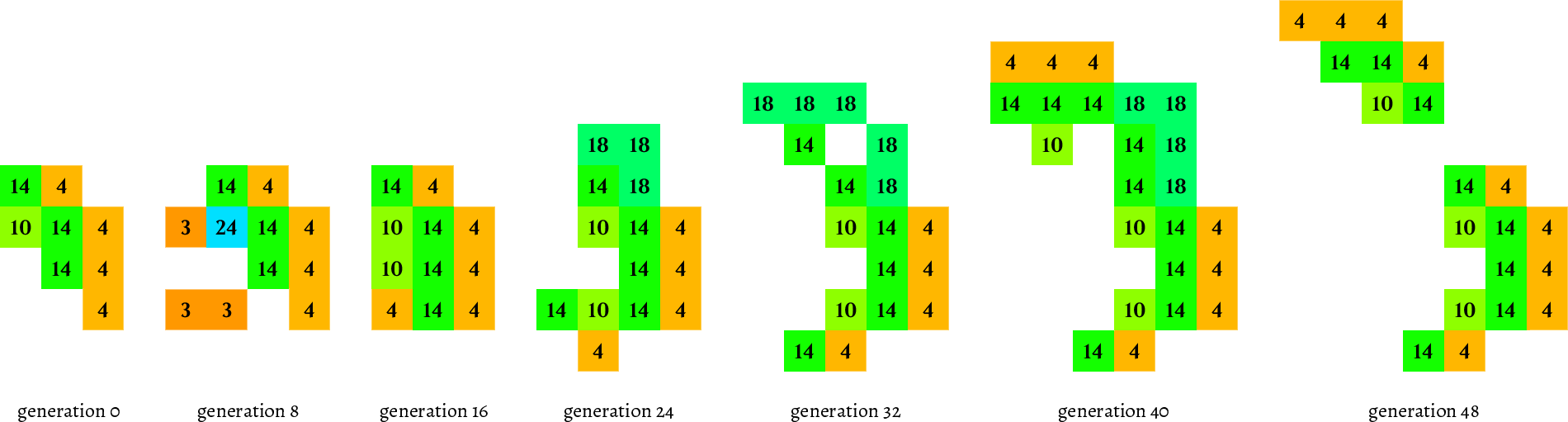
Speaking of devouring the plane, here's a quadratic replicator — reminiscent of something you might find in HighLife — running in +111/71/17:

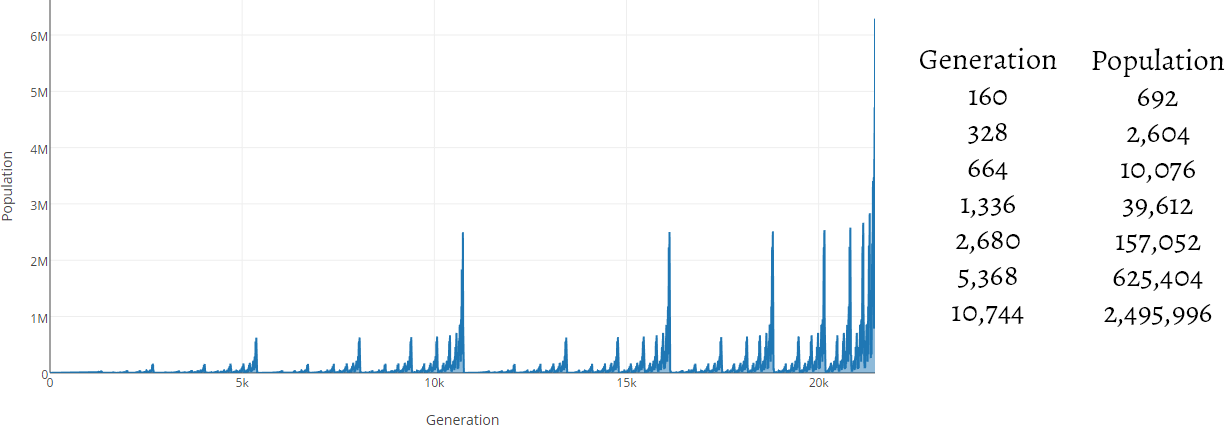
It has an initial population of just 4: two 111s and two 148s. It replicates every 21 generations, but collisions hinder its growth leading to a self-similar population curve that trends towards a quadrupling of population with each doubling of generations. And here's maybe the weirdest thing I've found, this self-replicating spaceship:

It runs in a variant of +10/3/11 that allows each cell to use its own value as well as the values of its neighbors to sum to the target number. It occurs with high frequency in random soups using this rule. It begins life with a population of just 8 (which can be trivially reduced to 6) and 48 generations later emits a reflected copy of its earlier self. What makes this replicator somewhat unusual, I think, is that the "mature" version of it — what remains after it has emitted a copy — can no longer replicate.
I haven't yet found a variant of the subset sum automata that matches the simultaneous unpredictability and intuitiveness of beloved and better studied CA like Life. There are, though, plenty of avenues still to be explored. A programmatic search for patterns in the ash of random soups would find plenty of stuff I didn't have the patience to look for in my hand-tuned experiments. I've been surprised by how different a rule's behavior can be when you only use orthogonal neighbors, or throw in a cell's own value as in my replicator example. There are a couple of non-divergent rules that use a fixed target number instead a target offset, and the new sums you can find by permitting negative numbers are probably worth checking into... but ultimately, the only thing I know about subset sum automata is that they make some pretty cool GIFs.